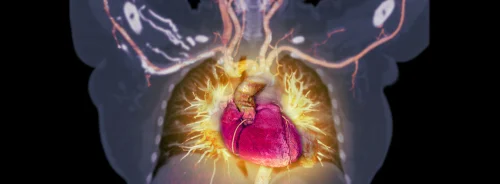
A new mathematical discovery may reduce the number of measuring points to one-sixth of the present level, meaning reduced exposure to radiation and faster medical imaging diagnostics. The theory called compressed sensing enables compressive sampling without having to look at the raw data first, according to physicists at the University of Oslo (UiO) who refer to the method as one of this century's most significant mathematical discoveries.
"The idea is to solve a task by involving as few measurements as possible. Whenever data capture is expensive, investment in this new mathematical approach may soon prove cost effective," says Professor Anders Malthe-Sørenssen at UiO's Department of Physics to the research magazine Apollon.
The highly sophisticated mathematical theory was introduced eight years ago by Australian-born mathematician Terence Tao, considered one of the world's most eminent mathematicians. Tao was only 24 when he, as the youngest person in history, was made professor of mathematics at the University of California 15 years ago. His theory, which is now generating interest amongst mathematicians all over the world, could bring about enormous savings in the health sector as well as in the oil industry.
Research fellow Andreas Solbrå, whose background is from mathematics, physics and calculation theory, is the first person at UiO to have put this theory to use. "Every measurement provides much more information than you think, provided you are smart about the sampling," according to Solbrå.
To illustrate the idea about performing as few measurements as possible, Solbrå points to a classic party brain teaser: There are 12 coins in front of you. They look identical, but one of them is counterfeit, and is either heavier or lighter than the other coins. You need to establish which one is the fake by using a pair of scales. Most readers will be able to identify the counterfeit coin in four or five weighings. Incredibly, it is also possible to solve the task in only three weighings.
This principle of sparse sampling underpins the idea conceived by Tao, says Solbrå. "Compressed sensing will enable you to calculate all the things you don't measure."
Faster Magnetic Resonance Imaging (MRI) Examinations
The method is highly calculation-intensive and may be used to reduce the number of measuring points used for MRI exams to one-sixth of the present level. This means that the MRI process may become six times faster than it is today.
"A simple examination of a knee takes 10 minutes. A cancer check-up may well take more than an hour," says magnetic resonance physicist Oliver Geier at Oslo University Hospital's Intervention Centre. "The socio-economic savings may be considerable if it is possible to reduce the time it takes to carry out an examination to one-sixth of the present level."
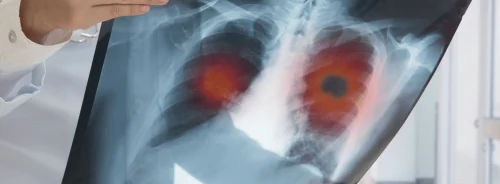
"There is also reason to believe that the new mathematical method can reduce the level of radiation from CT scans by five-sixths. The results remain just as good," Solbrå points out. CT scanners are not only expensive, but they also expose patients to doses of radiation which equal 10 years' natural background radiation.
Even if compressed sensing may be set to revolutionise medical diagnostics, the method is not well known. "Most hospitals will probably not have heard about it yet," thinks Solbrå.
A few years ago, Lucile Packard Children's Hospital Stanford (CA, USA) successfully tested the method by selecting the sampling points for the MRI scan.
There is a minor downside to the method. In order to compensate for the sparsity of measurements, more time must be spent on the calculations. "Today, doctors are able to analyse the medical images straight away. Compressed sensing will introduce a need for computer calculations before the results are ready," Solbrå explains.
People who are tasked with implementing the compressed sensing method in medical diagnostics must be highly skilled in maths as well as calculation theory. However, health service workers need not worry. "The maths is a one-off job," says Solbrå.
Geier at the Intervention Centre has never personally tested compressed sensing, but points out that the method is under development. One of the manufacturers of MRI scanners has already implemented the method. For now, however, the new imaging technique has been approved only for research purposes.
The new mathematical theory may also bring about major savings for the oil industry. Petroleum geologists depend on seismic measurements which involve sending sound waves into the ground. The sound waves are reflected off the various sediment layers and are then caught by microphones on the surface.
"Seismic sampling is very costly. Compressed sensing enables us to collect fewer data points while ending up with equally good information," says Prof. Malthe-Sørenssen.
Source: University of Oslo
Image Credit: Knut Løvås
"The idea is to solve a task by involving as few measurements as possible. Whenever data capture is expensive, investment in this new mathematical approach may soon prove cost effective," says Professor Anders Malthe-Sørenssen at UiO's Department of Physics to the research magazine Apollon.
The highly sophisticated mathematical theory was introduced eight years ago by Australian-born mathematician Terence Tao, considered one of the world's most eminent mathematicians. Tao was only 24 when he, as the youngest person in history, was made professor of mathematics at the University of California 15 years ago. His theory, which is now generating interest amongst mathematicians all over the world, could bring about enormous savings in the health sector as well as in the oil industry.
Research fellow Andreas Solbrå, whose background is from mathematics, physics and calculation theory, is the first person at UiO to have put this theory to use. "Every measurement provides much more information than you think, provided you are smart about the sampling," according to Solbrå.
To illustrate the idea about performing as few measurements as possible, Solbrå points to a classic party brain teaser: There are 12 coins in front of you. They look identical, but one of them is counterfeit, and is either heavier or lighter than the other coins. You need to establish which one is the fake by using a pair of scales. Most readers will be able to identify the counterfeit coin in four or five weighings. Incredibly, it is also possible to solve the task in only three weighings.
This principle of sparse sampling underpins the idea conceived by Tao, says Solbrå. "Compressed sensing will enable you to calculate all the things you don't measure."
Faster Magnetic Resonance Imaging (MRI) Examinations
The method is highly calculation-intensive and may be used to reduce the number of measuring points used for MRI exams to one-sixth of the present level. This means that the MRI process may become six times faster than it is today.
"A simple examination of a knee takes 10 minutes. A cancer check-up may well take more than an hour," says magnetic resonance physicist Oliver Geier at Oslo University Hospital's Intervention Centre. "The socio-economic savings may be considerable if it is possible to reduce the time it takes to carry out an examination to one-sixth of the present level."
"There is also reason to believe that the new mathematical method can reduce the level of radiation from CT scans by five-sixths. The results remain just as good," Solbrå points out. CT scanners are not only expensive, but they also expose patients to doses of radiation which equal 10 years' natural background radiation.
Even if compressed sensing may be set to revolutionise medical diagnostics, the method is not well known. "Most hospitals will probably not have heard about it yet," thinks Solbrå.
A few years ago, Lucile Packard Children's Hospital Stanford (CA, USA) successfully tested the method by selecting the sampling points for the MRI scan.
There is a minor downside to the method. In order to compensate for the sparsity of measurements, more time must be spent on the calculations. "Today, doctors are able to analyse the medical images straight away. Compressed sensing will introduce a need for computer calculations before the results are ready," Solbrå explains.
People who are tasked with implementing the compressed sensing method in medical diagnostics must be highly skilled in maths as well as calculation theory. However, health service workers need not worry. "The maths is a one-off job," says Solbrå.
Geier at the Intervention Centre has never personally tested compressed sensing, but points out that the method is under development. One of the manufacturers of MRI scanners has already implemented the method. For now, however, the new imaging technique has been approved only for research purposes.
The new mathematical theory may also bring about major savings for the oil industry. Petroleum geologists depend on seismic measurements which involve sending sound waves into the ground. The sound waves are reflected off the various sediment layers and are then caught by microphones on the surface.
"Seismic sampling is very costly. Compressed sensing enables us to collect fewer data points while ending up with equally good information," says Prof. Malthe-Sørenssen.
Source: University of Oslo
Image Credit: Knut Løvås
Latest Articles
MRI, Radiation, math, diagnostic imaging, mathematical theory, compressed sensing
A new mathematical discovery may reduce the number of measuring points to one-sixth of the present level, meaning reduced exposure to radiation and faster...