Explaining Linear COVID-19 Spread

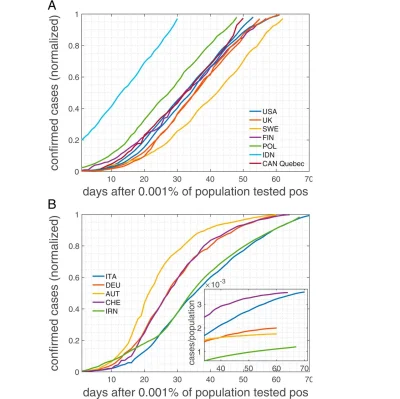
During the initial wave of the COVID-19 contagion, many countries recorded infection curves that were linear for extended time periods. This linear growth over an extended time interval is in contrast to the S-shaped curves expected from standard epidemiological models.

You might also like:Mobility, Connectivity and Pandemics of Modern World

"This observation is practically impossible to understand with traditional epidemiological models. These, to make them expressible in compact mathematical form, typically ignore the structure of real contact networks that are essential in the characteristic spreading dynamics of COVID-19," according to an article published in PNAS (Thurnera et al. 2020)

The article, authored by Medical University of Vienna researchers, points out that by taking some relevant network features into account, this linear growth 'phenomenon' can be better understood.

Social networks are known to hold the key to understanding details of epidemic outbreaks. These social or contact networks "are of a more involved structure," the authors explain, and include multilevel organisations, weak ties between communities, as well as "temporal aspects that suggest a degree of fluidity, however, with stable social cores."

The importance of contact networks in epidemiology, the authors note, has been recognised for almost two decades and has led to some significant contributions, such as the dependence of vaccination thresholds on network topology.

To explain the unusual linear growth pattern in COVID-19 cases, as observed in many countries (regardless of size and demographics), the authors have proposed a model based on the structure of contact networks. The model shows that, for any given transmission rate, there exists a critical number of social contacts below which linear infection curves must occur and above which the classical S-shaped curves appear.

Assuming realistic contact networks with a degree (number) of about 5, and assuming that lockdown measures would reduce that to household size (about 2.5), the model can reproduce actual infection curves with remarkable precision, according to the authors, who noted that countries with larger family structures might be closer to the critical degree, above which catastrophic epidemic spreading would occur.

In this study, the authors calibrated the model to realistic network parameters, transmission rates, and the time of being contagious and showed that realistic infection curves (in Austria and the U.S., as examples) emerge without any fine-tuning of parameters.

The onset of nonpharmaceutical interventions (e.g. lockdown) – and the associated reduction of the number/degree in the contact networks – determines the final size of the outbreak, which is well below the levels of herd immunity, according to the authors.

"In particular, we compare the United States and Austria, as examples for one country that initially did not impose measures and one that responded with a severe lockdown early on," the authors wrote. "Our findings question the applicability of standard compartmental models to describe the COVID-19 containment phase. The probability to observe linear growth in these is practically zero."

Source: PNAS

Image credit: Thurnera et al. 2020